【壓縮機網】＜——接上期＞
六、夾角γ為75°的計算
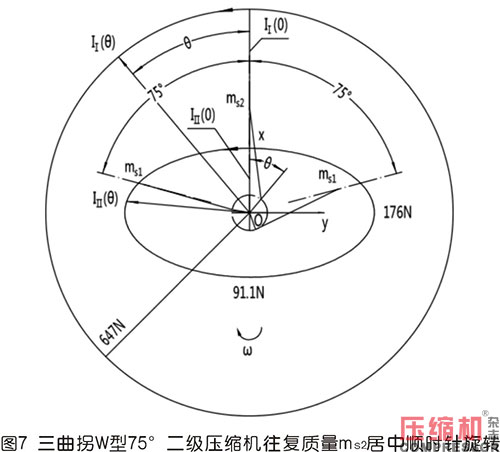
6.1用基礎理論分析圖7形式三曲拐順時針轉動時慣性力
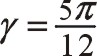
①一階慣性力的計算
按圖中順序依次寫成
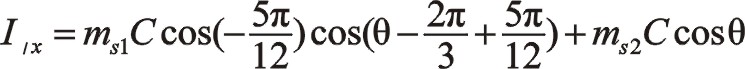
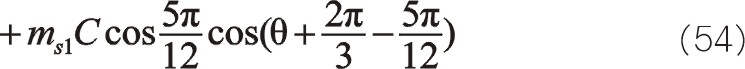
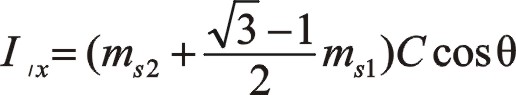
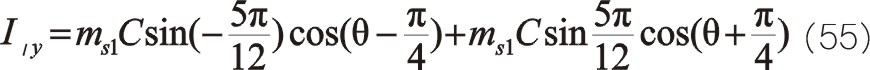
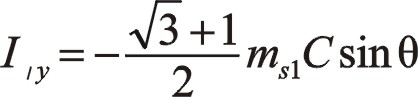
若兩質量相等則有
仿上一篇文章也可以寫成復數向量形式，則是如下
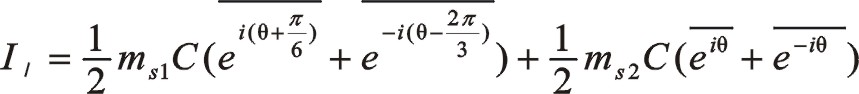
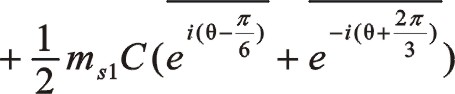
若不用共軛復數來表示，本篇文章以后的這樣的公式都這樣處理
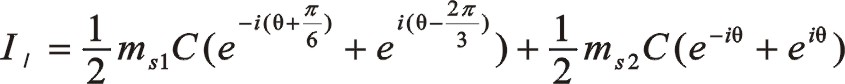
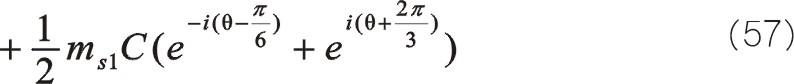
計算的結果與采用三角函數法相同。
可以得出三曲拐W型75°壓縮機一階慣性力是一個圓，這個圓與45°的一樣大，比60°的稍小些，式（56）與式（12）比較起來，一個是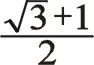 
而另一個是1.5。旋轉方向與曲柄反向。
②二階慣性力的計算
按圖中順序依次寫成
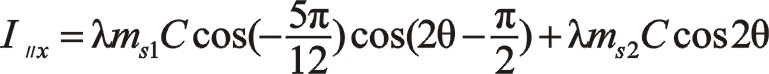
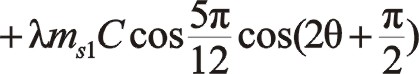
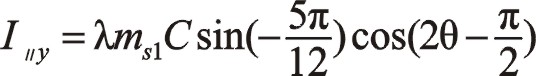
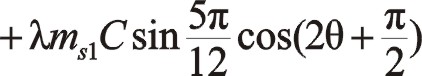
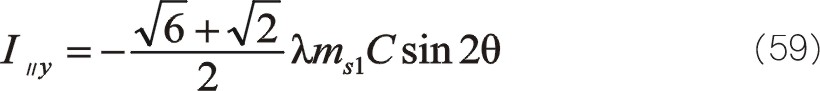
所以得出兩質量相等時，其二階慣性力是一橢圓，其大小比60°的大很多，旋轉方向與曲柄反向，橢圓的短長軸之比約為0.518。
由于圖中的坐標系就是建立在主方向對稱位置，因而也就無需進行旋轉變換。即使進行矩陣的旋轉變換，也就是乘以一個單位陣，運算后還等于自身；同樣的，所謂的一、二階慣性力的參數方程因考慮的主方向，所需要的代入變換也無需進行。
6.2用基礎理論分析圖8形式三曲拐順時針轉動時慣性力
①一階慣性力的計算
按圖中順序依次寫成
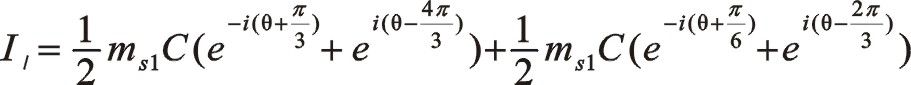
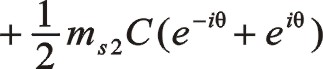
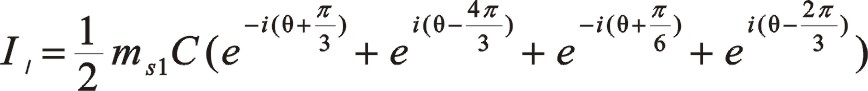
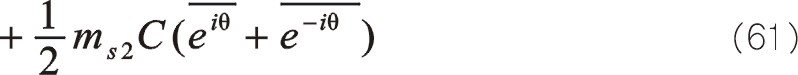
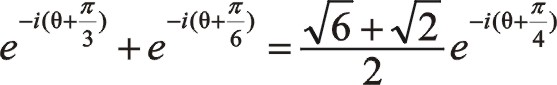
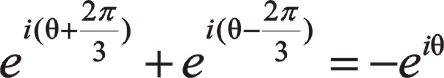
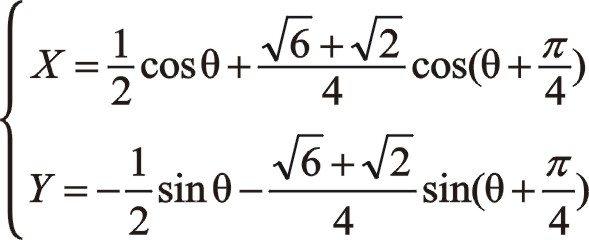
同樣的，也可以采用下式來計算
這說明，一階慣性力大小和旋轉方向還是圖7中那個圓，不過相位與居中分布的不一樣，往復質量ms2偏置分布不向自身旋轉時，一階慣性力的相位在0°與曲柄旋轉相位交角成30°，要注意的是這兩個矢量轉向相反，剛開始的時候這兩個矢量作相離運動，在165°的時候重合。這是因為從ms2偏置分布不向自身旋轉這個角度描述這兩個矢量的相位關系，從圖8中可以看出，該IⅠ(θ)的位置是從圖示的角度描述的，若我們換作中間的角度來看該問題，從圖中可以得出β角左右相等，這也顯然是異曲同工之妙。
從圖8看出，作負角30°旋轉變換到X″OY″坐標系中，圖8中沒有畫出該坐標系，則有
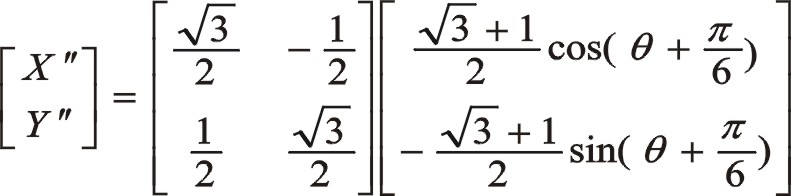
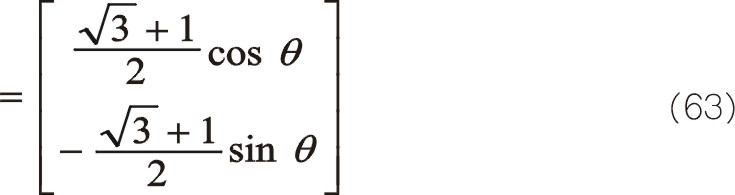
實際上它與圖7中描述的本質是一致的，簡單地說是圓和反相，僅相位角相差一個30°，這是因為氣缸夾角成75°分布。
我們這里來進行自變量的帶入變換。進行自變量的帶入變換的好處是：在進行計算機散點輸出慣性力圖像時，自動考慮到主方向位置，得出的一、二階慣性力圖像可以讓人們輕松地看出與其位置相對應，省去了將圖像作相應的角度的矩陣旋轉變換，這也是異曲同工之妙。以前曾講過，為計算方便，通常θ角的計入零點規定為ms2列活塞處于上死點的位置。文中得到的計算公式與選擇上面的計入零點無關。簡單地說，結構決定了慣性力的參數方程中的所有系數，這一點與解二元一次方程組只需要進行兩個行列式的比值運算類似。
怎樣作自變量的帶入變換呢，從圖8中我們建立α角，規定α角從中間位置到右邊列曲柄所轉到的位置。考慮到篇幅限制，我們統一認為三列往復質量相等來計算，三曲拐60°的沒有展開分析這一段，讀者有興趣可以自行回味。利用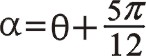 
，式（62）的換位公式即為
結合圖8，從換位公式（62′）可以看出，當α為45°時，也就是θ為－30°時，x軸達到最大而y軸為0，這是在xoy坐標系內得出的，也就是說，這時一階慣性力全部作用在x軸上也就是氣缸中心線上，亦即說明ms2列活塞的曲柄處于零位時，其一階慣性力位置落后曲柄位置30°。另外y軸的代數式有個負號說明反向旋轉。這與式（56）表達的意思一致。
③二階慣性力的計算
按圖中順序依次寫成
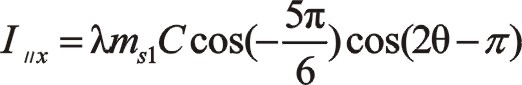
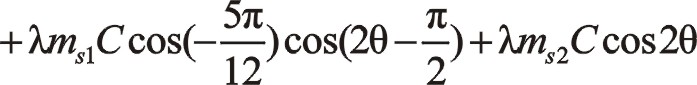
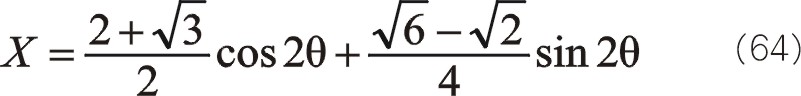
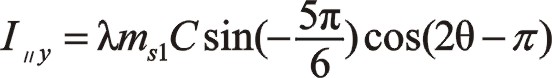
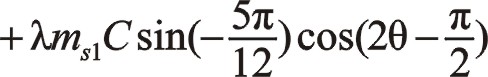
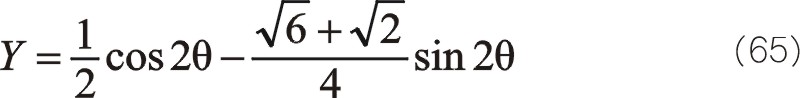
關于三曲拐W型75°順轉二階慣性力也有下列的方程運算，作正角15°旋轉變換
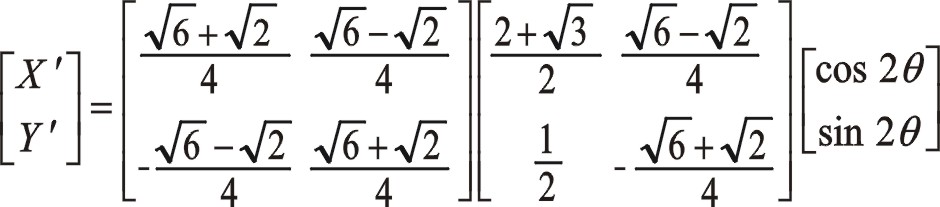
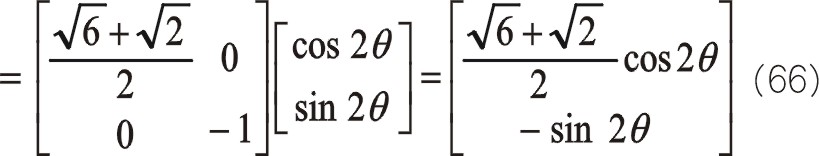
讀者也可以仿式（57）寫出其復數表達式來計算。
同樣的式（64）、（65）的換位公式為
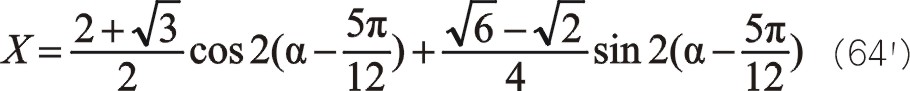
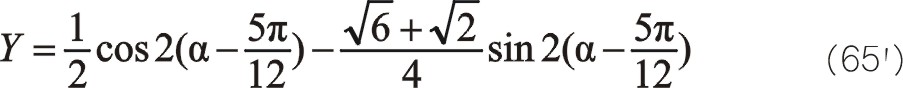
從式（66）發現，二階慣性力初始相位在水平方向，且與曲柄旋轉方向相反。
6.3用基礎理論分析圖9形式反時針轉動時慣性力
①一階慣性力的計算
按圖中順序依次寫成
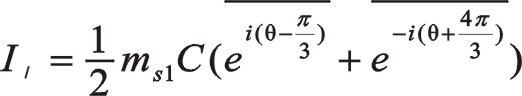
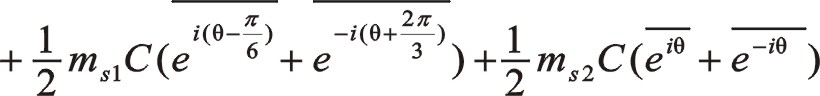
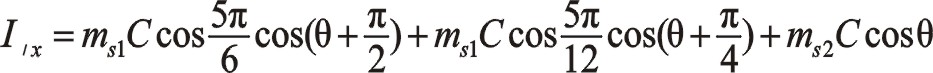
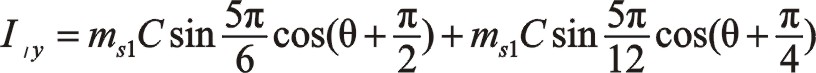
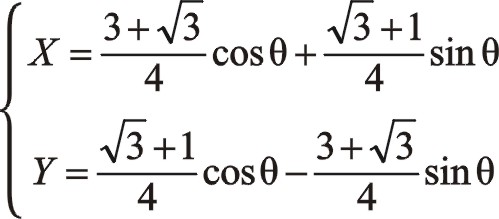
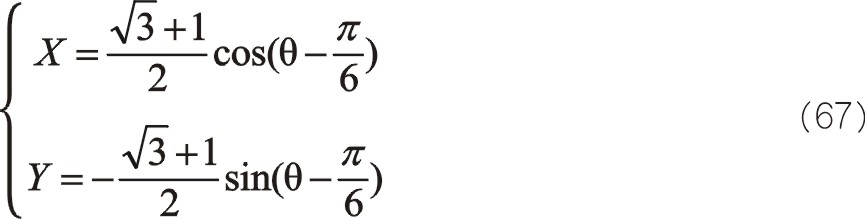
一階力大小和旋轉方向還是圖4中那個圓，從表面上看來其相位與居中分布的不一樣，往復質量ms2偏置分布并且向自身旋轉時，一階慣性力的相位在0°與曲柄相位相差30°，要注意的是這兩個矢量轉向相反，剛開始的時候這兩個矢量作相向運動，在15°的時候重合。圖6、圖5與圖4中描述的本質是一致的，簡單地說是圓和反相。
一階慣性力也可以作負角30°旋轉變換，此處不展開了。作負角30°旋轉變換得出的結果是最簡單的，實際上可以作任一角度的模為1的旋轉變換，不過得出的結果不是最簡單的，甚至很不容易看出其變化規律。以上所涉及的旋轉變換包括二階慣性力的旋轉變換都遵循這樣的原理。
同樣，我們從圖9中我們建立α角，規定α角從中間位置到右邊列曲柄所轉到的位置。這里統一認為三列往復質量相等來計算。利用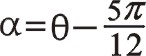 
式（67）的換位公式即為
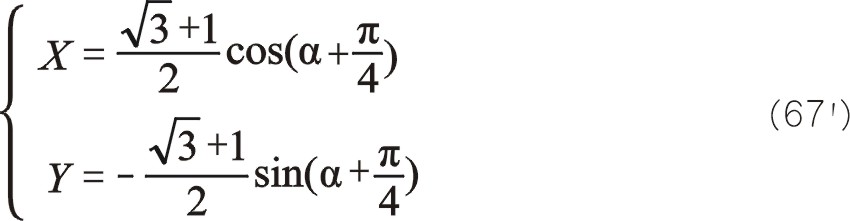
結合圖9，從換位公式（67′）可以看出，當α為－45°時，也就是θ為30°時，x軸達到最大而y軸為0，這是在xoy坐標系內得出的，也就是說，這時一階慣性力全部作用在x軸上也就是氣缸中心線上。另外y軸的代數式有個負號說明反向旋轉。這與式（56）表達的意思一致。
②二階慣性力的計算
按圖中順序依次寫成
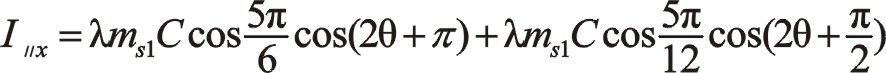
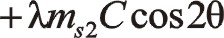
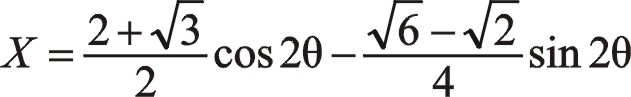
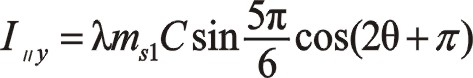
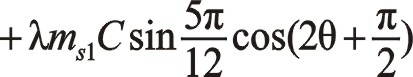
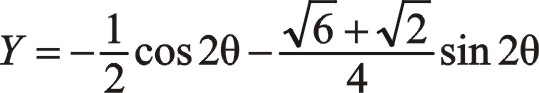
作負角15°旋轉變換
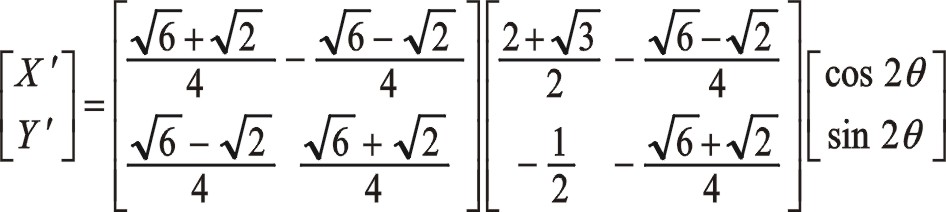
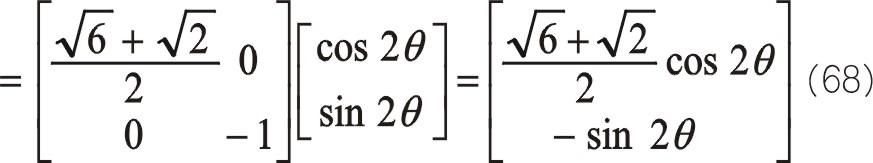
從式（68）發現，二階慣性力初始相位在水平方向，且與曲柄旋轉方向相反。讀者也可以仿式（57）寫出其復數表達式來計算。
讀者同樣可以寫出其換位公式，用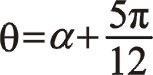 
帶入上面兩個公式中，此處不寫了。
6.4往復質量相等時圖7、圖8、圖9一致性驗算方程
由于圖9所畫的轉向是順時針，為弄明白坐標系的旋轉變換是正角變換還是負值變換，可以作圖9的鏡像圖，所以得到是負角75°變換，考慮到是均布三曲拐，所以新坐標系的開始角的度量關系如下
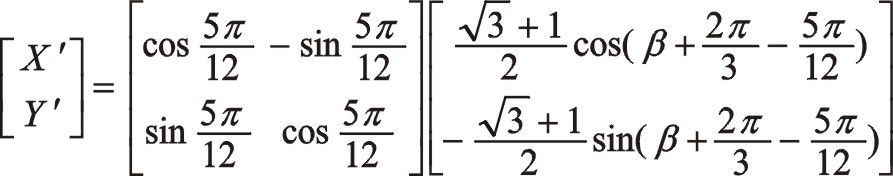
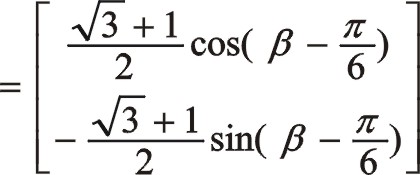
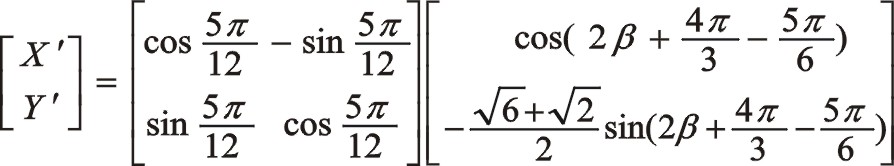
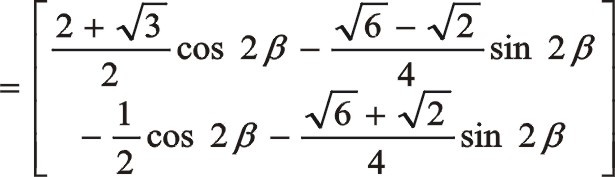
圖7與圖8之間的一致性方程留給讀者寫出。
6.5總結
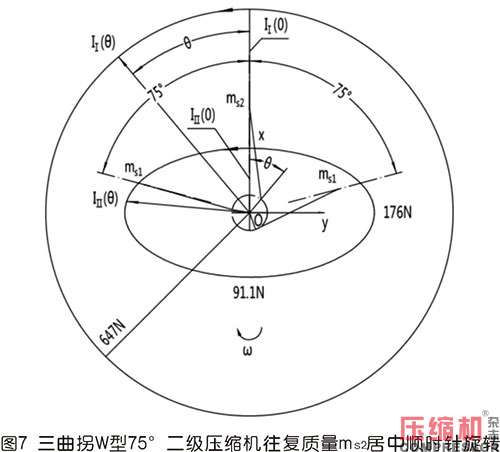
本處以安徽華晶機械有限公司生產的WW-0.9/10B-Q型全無油二級空壓機為模版，假定氣缸夾角為45°，計算其一、二階往復慣性力。此處先假定曲軸為三曲拐，三列往復質量相等，即ms為1.8kg，曲柄半徑為0.0375m，曲柄半徑連桿比λ為37.5/195，角速度ω為2π×(800/60)rad/s，現將上述結構參數分別代入上文中所列的相關公式中，運用計算機內EXCEL程序列表、繪圖計算分析，計算的結果繪制在上圖的圖7、圖8、圖9中，可以得到以下結論：
1）按圖7形式作居中順時針轉動，其一、二階慣性力矢端力圖如圖7所示。
計算結果表明：當按照圖7所示建立的直角坐標系xoy后，按照順時針轉θ角后，一階往復慣性力如IⅠ(θ)所示，它是一個圓；二階往復慣性力如IⅡ(θ)所示，它是一個很明顯的橢圓。一階慣性力的半徑長為647N，圖中顯示了當θ＝0°，一階慣性力的向量是IⅠ(0)，在這個位置曲柄矢與一階慣性力矢瞬時重合，隨后二者的方向矢量始終是關于豎直軸對稱。二階慣性力圖是一個標準的橢圓，二階慣性力的長半軸、短半軸為176N、91.1N，相比較45°分布的增大了很多，長軸始終在水平方向。圖中還顯示了當θ＝0°，二階慣性力的向量是IⅡ(0)，由于這種對稱布置，初始的二階慣性力向量與曲柄矢重合且同相，45°分布時初始的二階慣性力與曲柄重合反相，60°分布時初始的二階慣性力與曲柄重合同相，這些都是內在的均布三曲柄和外在的成一定角度分布的三氣缸所決定的。當曲軸旋轉一周時，二階慣性力是從IⅡ(0)位置開始沿著其二階力橢圓形式反時針轉動了2周，這不同于45°的情形，一階力則沿著外面的圓反時針轉動了1周。兩種慣性力的轉向與60°的等同。
2）按圖8形式作順時針轉動，其一、二階慣性力矢端力圖如圖8所示。
計算結果表明：當按照圖8所示建立的直角坐標系xoy后，按照順時針轉θ角后，一階往復慣性力如IⅠ(θ)所示，它是一個圓；二階往復慣性力如IⅡ(θ)所示，它是一個很明顯的橢圓。一階慣性力的半徑長為647N，圖中顯示了當θ＝0°，一階慣性力的向量是IⅠ(0)，在這個位置曲柄矢與一階慣性力矢瞬時不重合，而是在落后的30°的位置，剛開始在這個30°的位置內兩個矢量作相離運動。二階慣性力圖是一個標準的橢圓，二階慣性力的長半軸、短半軸為176N、91.1N，長軸始終在水平方向。圖中還顯示了當θ＝0°，二階慣性力的向量是IⅡ(0)，它正好在水平方向上，也就是在圖示的X′坐標軸方向的位置。當曲軸旋轉一周時，二階慣性力是從IⅡ(0)位置開始沿著其二階力橢圓形式反時針轉動了2周，而一階力則沿著外面的橢圓反時針轉動了1周。
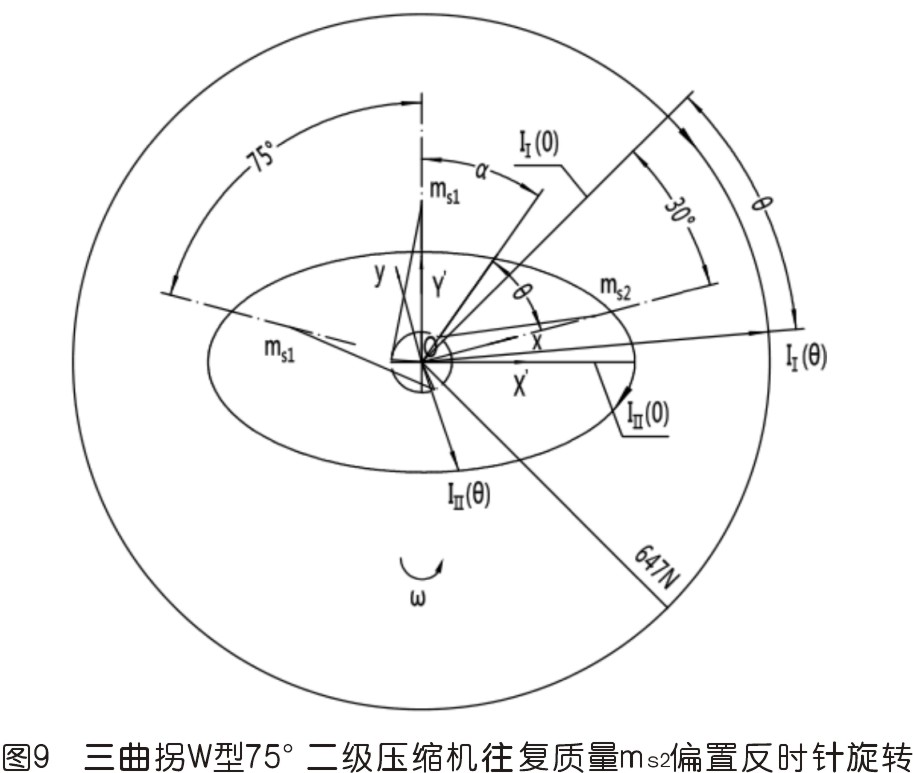
3）按圖9形式作反時針轉動，其一、二階慣性力矢端力圖如圖9所示。
這里需說明的是，一階慣性力圖還是圖7中的那個大圓，方向矢則逆著曲柄矢沿軌跡圖順時針變化。剛開始在圖中那個30°的位置內兩個矢量作相向運動；二階慣性力圖也類似這樣。并且圖8與圖9中起始的一階慣性力矢量IⅠ(0)不變，二階慣性力的初始矢量則相同。
三張圖實際上表達了同一種的一、二階往復慣性力的變化規律，根據式（56）、（60）、（62）、（66）、（67）、（68）得出，一階慣性力反向旋轉，大小是定值；二階慣性力也反向旋轉，大小成橢圓變化。同樣也給人一種“橫看成嶺側成峰，遠近高低各不同”的意蘊。
4）均布三曲拐W型夾角75°和45°的往復慣性力特性比較
①相同點
一階慣性力變化屬性完全相同，包括其大小和轉動屬性，都是與機器旋轉的方向相反，這不同于單曲拐的。如果都從居中的位置開始描述一階慣性力，則它們的參數方程完全相同。這一點決定了下面的這個事實：如果都從偏置的角度來描述這個問題，則75°時不向自身轉動時，與45°時向自身旋轉時，它們都是距曲柄矢向量30°范圍內背向旋轉，這兩種情形就是該兩個矢量互換。同樣，75°時向自身轉動時，與45°時不向自身旋轉時，它們都是距曲柄矢向量30°范圍內相向旋轉。由于這兩個方案一階慣性力變化屬性完全相同，則設計它們的平衡機構完全一樣，可以相互借用。
②不同點
二階慣性力變化屬性完全不同，75°時曲柄矢與二階慣性力矢轉向相反，其值較大；45°時曲柄矢與二階慣性力矢轉向相同而初始的相位成對角布置，其值較小，因而可以忽略無需設計專門的平衡機構來平衡二階往復慣性力。相比較起來我們所以說，三曲拐W型45°壓縮機是很有發展前途的壓縮機。
＜本文未完待續，更多精彩內容見下期！＞
參考文獻
(1)陸鵬程，復數法分析研究W型壓縮機往復慣性力(一～四)[J]，壓縮機，2024.8～11期
(2)宋瑞林，氣缸夾角為60°的V6車用發動機往復慣性力的平衡分析，[J]，汽車技術，1988.8
(3)李松虎，3W型活塞壓縮機往復慣性力的分析，[J]，壓縮機技術，1987.3
(4)陸鵬程，張光勝，三星型壓縮機振動問題研究，[J]，安徽工程科技學院學報，2009.1
(5)王再順，夾角為90°的V型壓縮機往復慣性力平衡的探討，[J]，壓縮機技術，1986.2
作者簡介
陸鵬程，男，安徽桐城人，海軍工程大學在職碩士畢業。現在中國人民解放軍第四八一二工廠，安徽華晶機械有限公司工作，高級工程師。研究方向：壓縮機研究與強度設計。
【壓縮機網】＜——接上期＞
六、夾角γ為75°的計算
6.1用基礎理論分析圖7形式三曲拐順時針轉動時慣性力
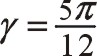
①一階慣性力的計算
按圖中順序依次寫成
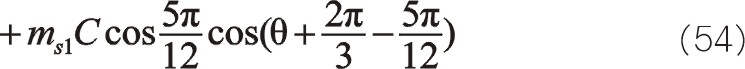
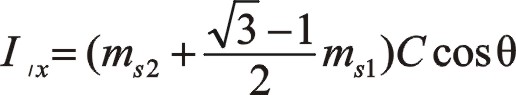
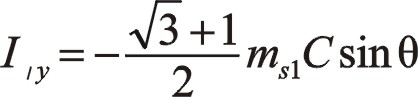
若兩質量相等則有
仿上一篇文章也可以寫成復數向量形式，則是如下
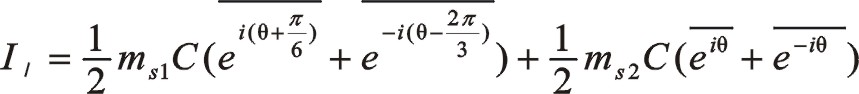
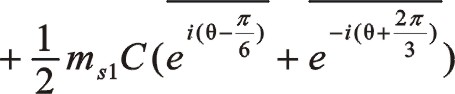
若不用共軛復數來表示，本篇文章以后的這樣的公式都這樣處理
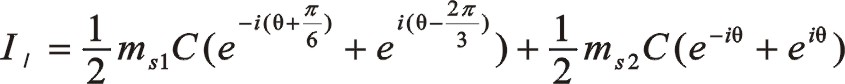
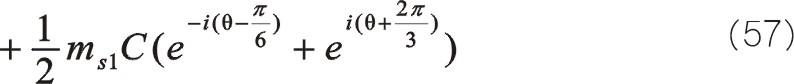
計算的結果與采用三角函數法相同。
可以得出三曲拐W型75°壓縮機一階慣性力是一個圓，這個圓與45°的一樣大，比60°的稍小些，式（56）與式（12）比較起來，一個是 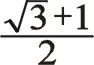而另一個是1.5。旋轉方向與曲柄反向。
②二階慣性力的計算
按圖中順序依次寫成
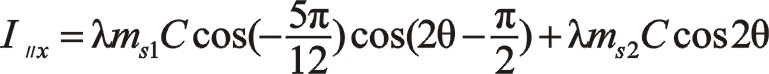
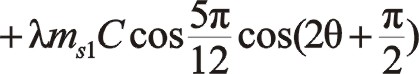
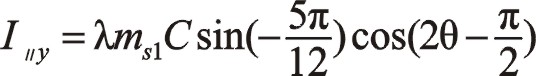
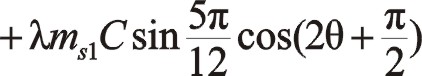
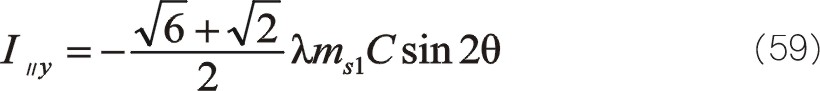
所以得出兩質量相等時，其二階慣性力是一橢圓，其大小比60°的大很多，旋轉方向與曲柄反向，橢圓的短長軸之比約為0.518。
由于圖中的坐標系就是建立在主方向對稱位置，因而也就無需進行旋轉變換。即使進行矩陣的旋轉變換，也就是乘以一個單位陣，運算后還等于自身；同樣的，所謂的一、二階慣性力的參數方程因考慮的主方向，所需要的代入變換也無需進行。
6.2用基礎理論分析圖8形式三曲拐順時針轉動時慣性力
①一階慣性力的計算
按圖中順序依次寫成
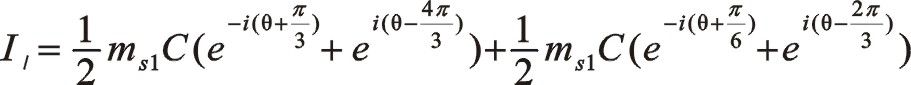
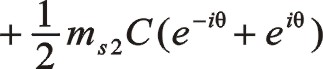
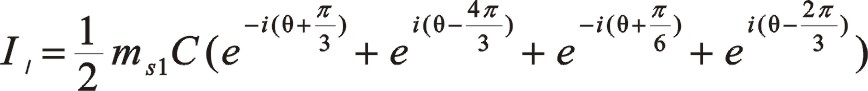
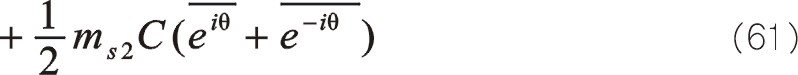
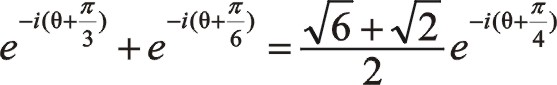
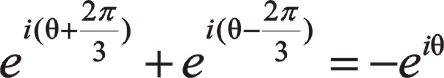
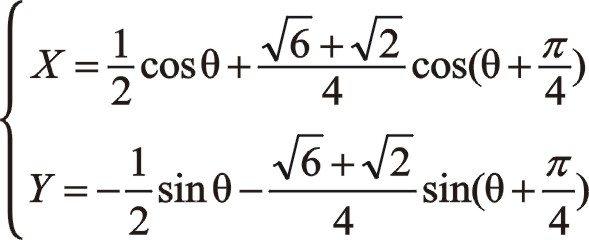
同樣的，也可以采用下式來計算
這說明，一階慣性力大小和旋轉方向還是圖7中那個圓，不過相位與居中分布的不一樣，往復質量ms2偏置分布不向自身旋轉時，一階慣性力的相位在0°與曲柄旋轉相位交角成30°，要注意的是這兩個矢量轉向相反，剛開始的時候這兩個矢量作相離運動，在165°的時候重合。這是因為從ms2偏置分布不向自身旋轉這個角度描述這兩個矢量的相位關系，從圖8中可以看出，該IⅠ(θ)的位置是從圖示的角度描述的，若我們換作中間的角度來看該問題，從圖中可以得出β角左右相等，這也顯然是異曲同工之妙。
從圖8看出，作負角30°旋轉變換到X″OY″坐標系中，圖8中沒有畫出該坐標系，則有
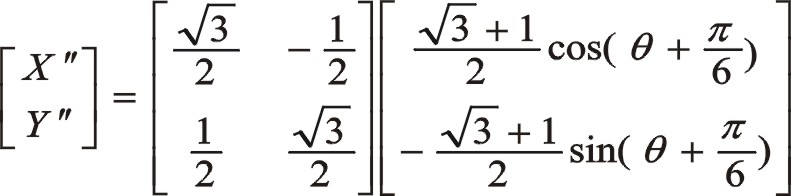
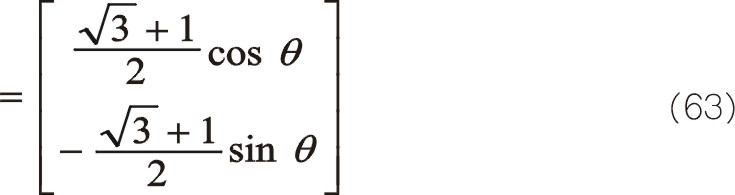
實際上它與圖7中描述的本質是一致的，簡單地說是圓和反相，僅相位角相差一個30°，這是因為氣缸夾角成75°分布。
我們這里來進行自變量的帶入變換。進行自變量的帶入變換的好處是：在進行計算機散點輸出慣性力圖像時，自動考慮到主方向位置，得出的一、二階慣性力圖像可以讓人們輕松地看出與其位置相對應，省去了將圖像作相應的角度的矩陣旋轉變換，這也是異曲同工之妙。以前曾講過，為計算方便，通常θ角的計入零點規定為ms2列活塞處于上死點的位置。文中得到的計算公式與選擇上面的計入零點無關。簡單地說，結構決定了慣性力的參數方程中的所有系數，這一點與解二元一次方程組只需要進行兩個行列式的比值運算類似。
怎樣作自變量的帶入變換呢，從圖8中我們建立α角，規定α角從中間位置到右邊列曲柄所轉到的位置。考慮到篇幅限制，我們統一認為三列往復質量相等來計算，三曲拐60°的沒有展開分析這一段，讀者有興趣可以自行回味。利用 ，式（62）的換位公式即為
結合圖8，從換位公式（62′）可以看出，當α為45°時，也就是θ為－30°時，x軸達到最大而y軸為0，這是在xoy坐標系內得出的，也就是說，這時一階慣性力全部作用在x軸上也就是氣缸中心線上，亦即說明ms2列活塞的曲柄處于零位時，其一階慣性力位置落后曲柄位置30°。另外y軸的代數式有個負號說明反向旋轉。這與式（56）表達的意思一致。
③二階慣性力的計算
按圖中順序依次寫成
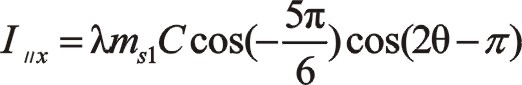
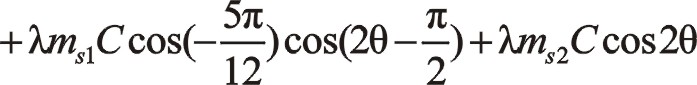
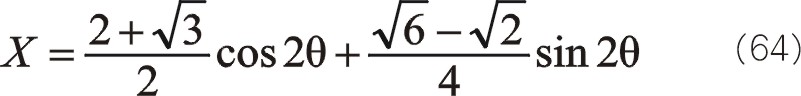
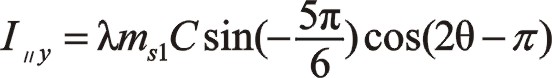
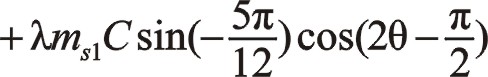
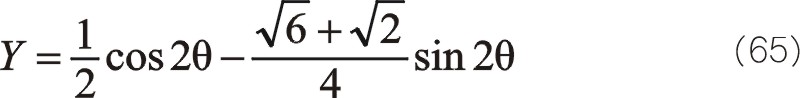
關于三曲拐W型75°順轉二階慣性力也有下列的方程運算，作正角15°旋轉變換
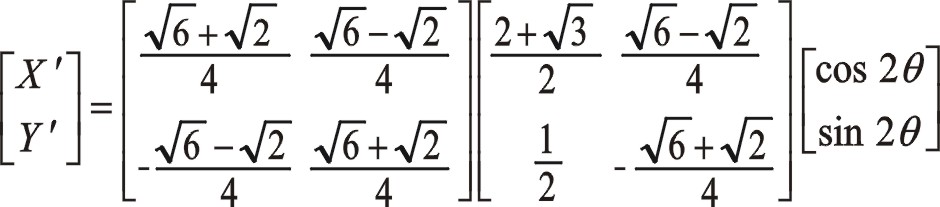
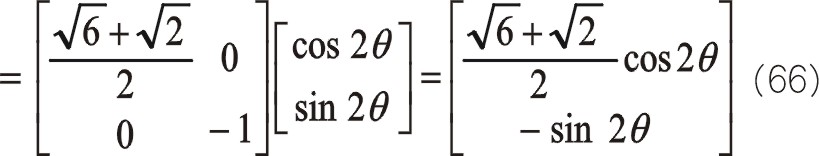
讀者也可以仿式（57）寫出其復數表達式來計算。
同樣的式（64）、（65）的換位公式為
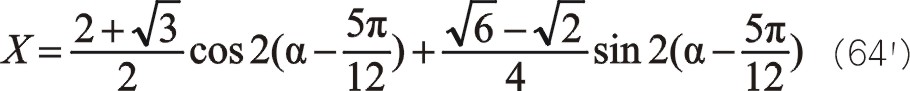
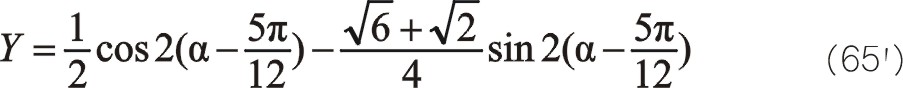
從式（66）發現，二階慣性力初始相位在水平方向，且與曲柄旋轉方向相反。
6.3用基礎理論分析圖9形式反時針轉動時慣性力
①一階慣性力的計算
按圖中順序依次寫成
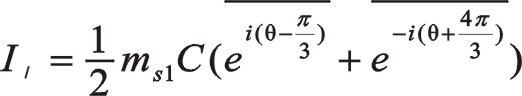
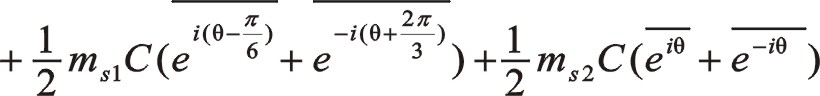
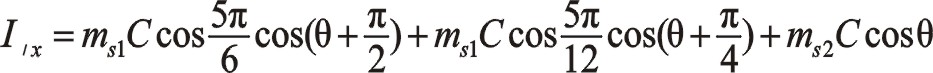
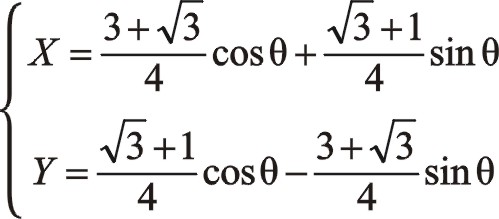
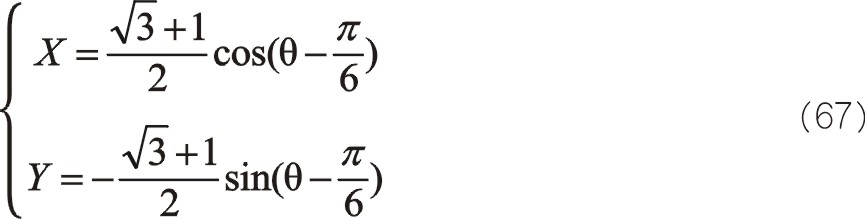
一階力大小和旋轉方向還是圖4中那個圓，從表面上看來其相位與居中分布的不一樣，往復質量ms2偏置分布并且向自身旋轉時，一階慣性力的相位在0°與曲柄相位相差30°，要注意的是這兩個矢量轉向相反，剛開始的時候這兩個矢量作相向運動，在15°的時候重合。圖6、圖5與圖4中描述的本質是一致的，簡單地說是圓和反相。
一階慣性力也可以作負角30°旋轉變換，此處不展開了。作負角30°旋轉變換得出的結果是最簡單的，實際上可以作任一角度的模為1的旋轉變換，不過得出的結果不是最簡單的，甚至很不容易看出其變化規律。以上所涉及的旋轉變換包括二階慣性力的旋轉變換都遵循這樣的原理。
同樣，我們從圖9中我們建立α角，規定α角從中間位置到右邊列曲柄所轉到的位置。這里統一認為三列往復質量相等來計算。利用 式（67）的換位公式即為
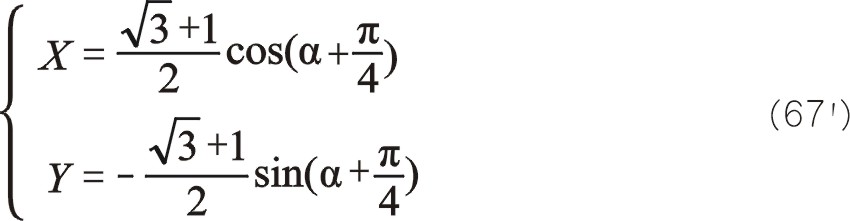
結合圖9，從換位公式（67′）可以看出，當α為－45°時，也就是θ為30°時，x軸達到最大而y軸為0，這是在xoy坐標系內得出的，也就是說，這時一階慣性力全部作用在x軸上也就是氣缸中心線上。另外y軸的代數式有個負號說明反向旋轉。這與式（56）表達的意思一致。
②二階慣性力的計算
按圖中順序依次寫成
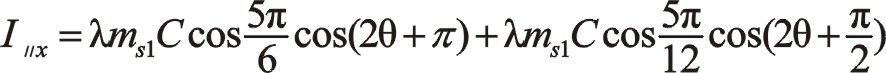
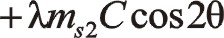
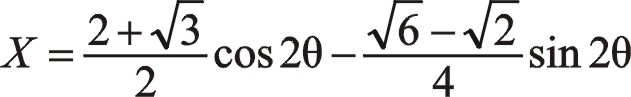
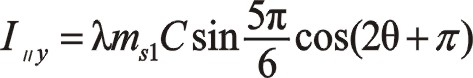
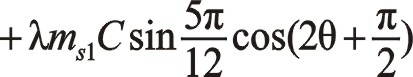
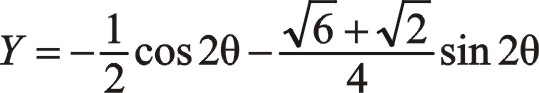
作負角15°旋轉變換
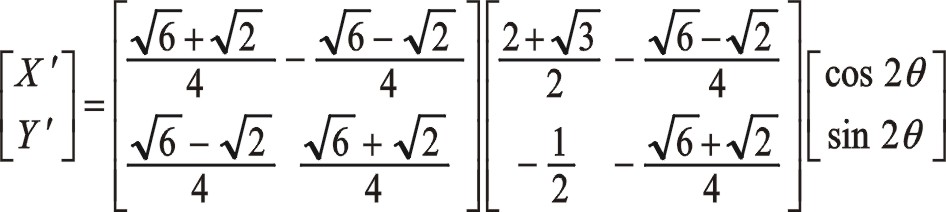
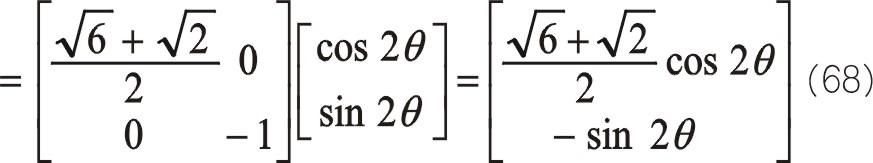
從式（68）發現，二階慣性力初始相位在水平方向，且與曲柄旋轉方向相反。讀者也可以仿式（57）寫出其復數表達式來計算。
讀者同樣可以寫出其換位公式，用 帶入上面兩個公式中，此處不寫了。
6.4往復質量相等時圖7、圖8、圖9一致性驗算方程
由于圖9所畫的轉向是順時針，為弄明白坐標系的旋轉變換是正角變換還是負值變換，可以作圖9的鏡像圖，所以得到是負角75°變換，考慮到是均布三曲拐，所以新坐標系的開始角的度量關系如下
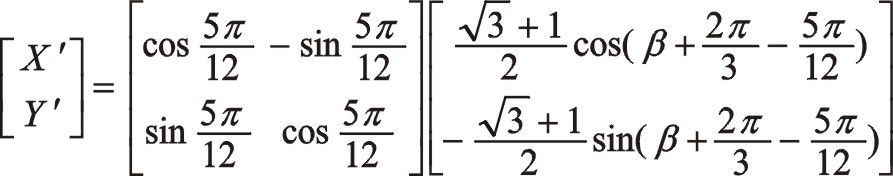
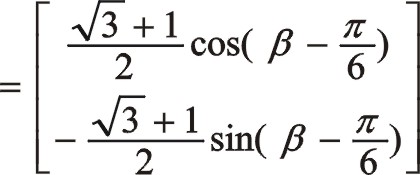
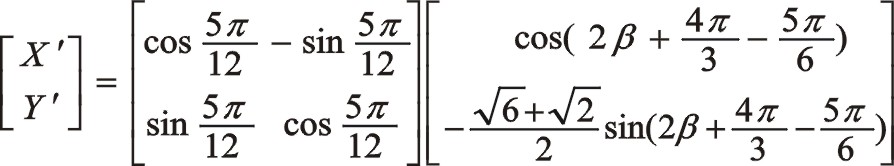
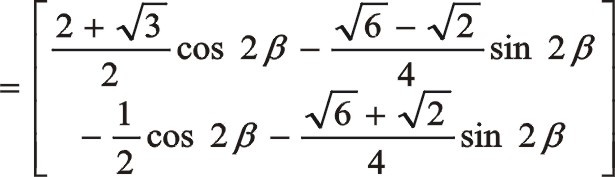
圖7與圖8之間的一致性方程留給讀者寫出。
6.5總結
本處以安徽華晶機械有限公司生產的WW-0.9/10B-Q型全無油二級空壓機為模版，假定氣缸夾角為45°，計算其一、二階往復慣性力。此處先假定曲軸為三曲拐，三列往復質量相等，即ms為1.8kg，曲柄半徑為0.0375m，曲柄半徑連桿比λ為37.5/195，角速度ω為2π×(800/60)rad/s，現將上述結構參數分別代入上文中所列的相關公式中，運用計算機內EXCEL程序列表、繪圖計算分析，計算的結果繪制在上圖的圖7、圖8、圖9中，可以得到以下結論：
1）按圖7形式作居中順時針轉動，其一、二階慣性力矢端力圖如圖7所示。
計算結果表明：當按照圖7所示建立的直角坐標系xoy后，按照順時針轉θ角后，一階往復慣性力如IⅠ(θ)所示，它是一個圓；二階往復慣性力如IⅡ(θ)所示，它是一個很明顯的橢圓。一階慣性力的半徑長為647N，圖中顯示了當θ＝0°，一階慣性力的向量是IⅠ(0)，在這個位置曲柄矢與一階慣性力矢瞬時重合，隨后二者的方向矢量始終是關于豎直軸對稱。二階慣性力圖是一個標準的橢圓，二階慣性力的長半軸、短半軸為176N、91.1N，相比較45°分布的增大了很多，長軸始終在水平方向。圖中還顯示了當θ＝0°，二階慣性力的向量是IⅡ(0)，由于這種對稱布置，初始的二階慣性力向量與曲柄矢重合且同相，45°分布時初始的二階慣性力與曲柄重合反相，60°分布時初始的二階慣性力與曲柄重合同相，這些都是內在的均布三曲柄和外在的成一定角度分布的三氣缸所決定的。當曲軸旋轉一周時，二階慣性力是從IⅡ(0)位置開始沿著其二階力橢圓形式反時針轉動了2周，這不同于45°的情形，一階力則沿著外面的圓反時針轉動了1周。兩種慣性力的轉向與60°的等同。
2）按圖8形式作順時針轉動，其一、二階慣性力矢端力圖如圖8所示。
計算結果表明：當按照圖8所示建立的直角坐標系xoy后，按照順時針轉θ角后，一階往復慣性力如IⅠ(θ)所示，它是一個圓；二階往復慣性力如IⅡ(θ)所示，它是一個很明顯的橢圓。一階慣性力的半徑長為647N，圖中顯示了當θ＝0°，一階慣性力的向量是IⅠ(0)，在這個位置曲柄矢與一階慣性力矢瞬時不重合，而是在落后的30°的位置，剛開始在這個30°的位置內兩個矢量作相離運動。二階慣性力圖是一個標準的橢圓，二階慣性力的長半軸、短半軸為176N、91.1N，長軸始終在水平方向。圖中還顯示了當θ＝0°，二階慣性力的向量是IⅡ(0)，它正好在水平方向上，也就是在圖示的X′坐標軸方向的位置。當曲軸旋轉一周時，二階慣性力是從IⅡ(0)位置開始沿著其二階力橢圓形式反時針轉動了2周，而一階力則沿著外面的橢圓反時針轉動了1周。
3）按圖9形式作反時針轉動，其一、二階慣性力矢端力圖如圖9所示。
這里需說明的是，一階慣性力圖還是圖7中的那個大圓，方向矢則逆著曲柄矢沿軌跡圖順時針變化。剛開始在圖中那個30°的位置內兩個矢量作相向運動；二階慣性力圖也類似這樣。并且圖8與圖9中起始的一階慣性力矢量IⅠ(0)不變，二階慣性力的初始矢量則相同。
三張圖實際上表達了同一種的一、二階往復慣性力的變化規律，根據式（56）、（60）、（62）、（66）、（67）、（68）得出，一階慣性力反向旋轉，大小是定值；二階慣性力也反向旋轉，大小成橢圓變化。同樣也給人一種“橫看成嶺側成峰，遠近高低各不同”的意蘊。
4）均布三曲拐W型夾角75°和45°的往復慣性力特性比較
①相同點
一階慣性力變化屬性完全相同，包括其大小和轉動屬性，都是與機器旋轉的方向相反，這不同于單曲拐的。如果都從居中的位置開始描述一階慣性力，則它們的參數方程完全相同。這一點決定了下面的這個事實：如果都從偏置的角度來描述這個問題，則75°時不向自身轉動時，與45°時向自身旋轉時，它們都是距曲柄矢向量30°范圍內背向旋轉，這兩種情形就是該兩個矢量互換。同樣，75°時向自身轉動時，與45°時不向自身旋轉時，它們都是距曲柄矢向量30°范圍內相向旋轉。由于這兩個方案一階慣性力變化屬性完全相同，則設計它們的平衡機構完全一樣，可以相互借用。
②不同點
二階慣性力變化屬性完全不同，75°時曲柄矢與二階慣性力矢轉向相反，其值較大；45°時曲柄矢與二階慣性力矢轉向相同而初始的相位成對角布置，其值較小，因而可以忽略無需設計專門的平衡機構來平衡二階往復慣性力。相比較起來我們所以說，三曲拐W型45°壓縮機是很有發展前途的壓縮機。
＜本文未完待續，更多精彩內容見下期！＞
參考文獻
(1)陸鵬程，復數法分析研究W型壓縮機往復慣性力(一～四)[J]，壓縮機，2024.8～11期
(2)宋瑞林，氣缸夾角為60°的V6車用發動機往復慣性力的平衡分析，[J]，汽車技術，1988.8
(3)李松虎，3W型活塞壓縮機往復慣性力的分析，[J]，壓縮機技術，1987.3
(4)陸鵬程，張光勝，三星型壓縮機振動問題研究，[J]，安徽工程科技學院學報，2009.1
(5)王再順，夾角為90°的V型壓縮機往復慣性力平衡的探討，[J]，壓縮機技術，1986.2
作者簡介
陸鵬程，男，安徽桐城人，海軍工程大學在職碩士畢業。現在中國人民解放軍第四八一二工廠，安徽華晶機械有限公司工作，高級工程師。研究方向：壓縮機研究與強度設計。
網友評論
條評論
最新評論